Voxelization in Unity

| Comments

This post was originally published on my previous blog

A few words on Voxelization and SAT

In this post we will create a script for voxelize any kind of mesh in unity. Voxelization could be useful in physical simulations, terrain representation and every situation where we need to manipulate the hollow inside of a mesh. A great post about Voxelization can be found “here”, on Wolfire blog. The post explains how the voxelization of a triangle mesh is done in Overgrowth, we will use the same method in unity.

The creation of a voxel model that reproduces the mesh is achived trough a 3d grid of cubes and an intersection test for each triangle against each cube. The author states that he uses a AABB-AABB intersection test to check if a cube and a triangle are intersected. This is very fast and appropriate for most situations, but we want the general solution.

A slower but precise way to test the intersection is to use the Separating Axis Theorem. This paper explains the use of the SAT for Triangle-AABB intersection.

An implementation in C++ of this algorithm was written by Mike Vandelay and can be found planet-source-code.com. I rewrote the same code in unityscript.

Basically the SAT works like this

Take 13 axes: 3 axes are the cube face normals, 1 axis is the triangle face normal, 9 are the dot product between the first 3 axes and the triangles edges.

Project the AABB and the triangle on each axis. If the projections intersects on an axis, then the AABB and the triangle are intersected, otherwise they aren’t. here a much more detailed explanation of the SAT.

Now, let’s see how implement all this in unity.

Mesh Voxelization

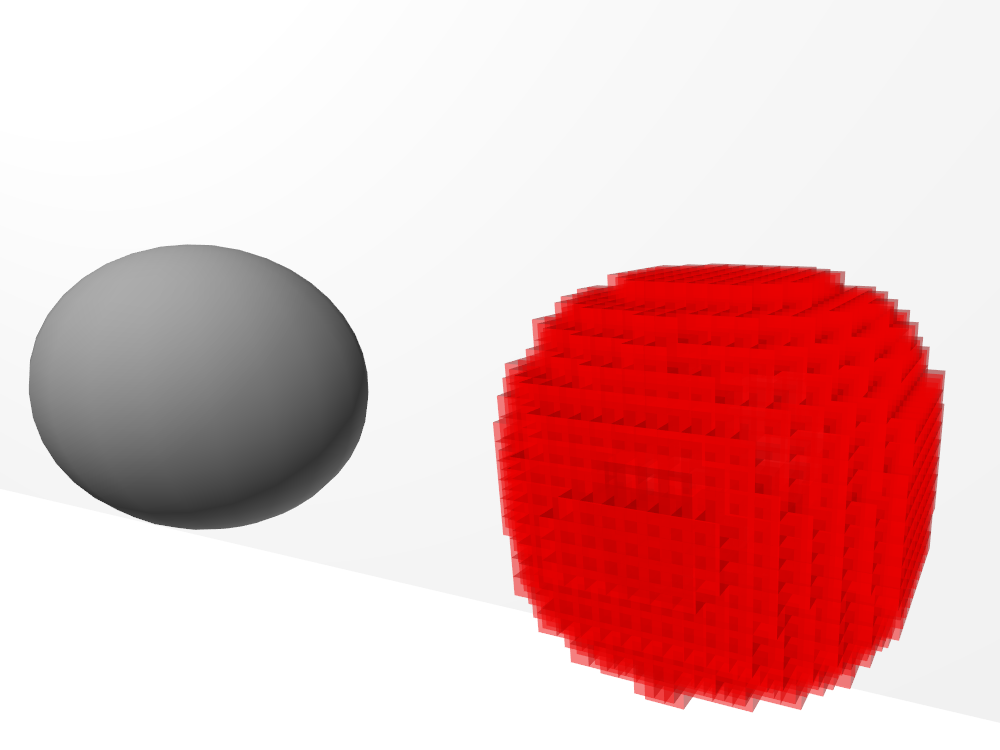
voxelized sphere

The complete script for voxelization can be found here on my github.

We are going to use a grid for creating a voxel model. Each Grid is formed by cubes of the same size, these are the grid properties:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

public class AABCGrid {

private var side : float;
private var width : short;
private var height : short;
private var depth : short;
private var origin : Vector3;
private var cubeSet : boolean[,,];
private var cubeNormalSum : short[,,];
private var debug = false;

...
}

/*
AABC stands for Axis Aligned Bounding Cube.
For performance purpose, I didn't add a 3 dimension array of AABCs, otherwise each cube had to store the side length, the set value etc...
However an AABC class is defined, but only for external use, while inside the AABCGrid class everything is evaluated starting from the class properties.
e.g. to obtain the vertices of a cube is it possible to use the method
AABCGrid.GetAABCCorners(x : short, y : short, z : short) : Vector3[]
or the method AABC.GetCorners().
The AABC.GetCorners() is actually defined like this:
*/
public function GetCorners(x : short, y : short, z : short) : Vector3[] {
    // grid is a reference to an AABCGrid
    return grid.GetAABCCorners(x, y, z);
}

All the public method call a CheckBound() function that check if the cube specified by the x, y, z variable is inside the grid, then the real implementation of the method is called. e.g.

1
2
3
4
5
6
7
8

public function IsAABCSet(x : short, y : short, z : short) : boolean {
   CheckBounds(x, y, z);
   return IsAABCSetUnchecked(x, y, z);
}

protected function IsAABCSetUnchecked(x : short, y : short, z : short) : boolean {
   return cubeSet[x, y, z];
}

Off course, inside the AABCGrid class and in the possible inheritors, only the unchecked method should be called for faster code.

Creating the voxel shell

Once the grid is defined, we need to ‘set’ all the cubes that are intersected by a triangle of the mesh. This is done in the AABCGrid.FillGridWithGameObjectMeshShell() method.

The result will be a voxel shell, an empty shape that reproduces the mesh.

Ignore the part relative to the normals of the triangles, I’m going to explain that later.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

public function FillGridWithGameObjectMeshShell(gameObj : GameObject, storeNormalSum : boolean) {
    var gameObjMesh = gameObj.GetComponent(MeshFilter).mesh;
    var gameObjTransf = gameObj.transform;
    var triangle = new Vector3[3];
    var startTime = Time.realtimeSinceStartup;
    var meshVertices = gameObjMesh.vertices;
    var meshTriangles = gameObjMesh.triangles;
    var meshTrianglesCount = meshTriangles.length / 3;
    var x : short;
    var y : short;
    var z : short;
    var ignoreNormalRange = 0;
    // In this method we can also evaluate stores the normals of the triangles 
    // that intersect the cube.
    if (storeNormalSum) {
        cubeNormalSum = new short [width, height, depth];
    }
    if(debug) {
        Debug.Log("Start:");
        Debug.Log("Time: " + startTime);
        Debug.Log("     Mesh Description: ");
        Debug.Log("Name: " + gameObjMesh.name);
        Debug.Log("Triangles: " + meshTrianglesCount);
        Debug.Log("Local AABB size: " + gameObjMesh.bounds.size);
        Debug.Log("     AABCGrid Description:");
        Debug.Log("Size: " + width + ',' + height + ',' + depth);
    }

    // For each triangle, perform SAT intersection check with the AABCs within the triangle AABB.
    for (var i = 0; i < meshTrianglesCount; ++i) {
        triangle[0] = gameObjTransf.TransformPoint(meshVertices[meshTriangles[i * 3]]);
        triangle[1] = gameObjTransf.TransformPoint(meshVertices[meshTriangles[i * 3 + 1]]);
        triangle[2] = gameObjTransf.TransformPoint(meshVertices[meshTriangles[i * 3 + 2]]);
        // Find the triangle AABB, select a sub grid.
        var startX = Mathf.Floor((Mathf.Min([triangle[0].x, triangle[1].x, triangle[2].x]) - origin.x) / side);
        var startY = Mathf.Floor((Mathf.Min([triangle[0].y, triangle[1].y, triangle[2].y]) - origin.y) / side);
        var startZ = Mathf.Floor((Mathf.Min([triangle[0].z, triangle[1].z, triangle[2].z]) - origin.z) / side);
        var endX = Mathf.Ceil((Mathf.Max([triangle[0].x, triangle[1].x, triangle[2].x]) - origin.x) / side);
        var endY = Mathf.Ceil((Mathf.Max([triangle[0].y, triangle[1].y, triangle[2].y]) - origin.y) / side);
        var endZ = Mathf.Ceil((Mathf.Max([triangle[0].z, triangle[1].z, triangle[2].z]) - origin.z) / side);
        if (storeNormalSum) {
            for (x = startX; x <= endX; ++x) {
                for (y = startY; y <= endY; ++y) {
                    for (z = startZ; z <= endZ; ++z) {
                        if (TriangleIntersectAABC(triangle, x, y, z)) {
                            var triangleNormal = GetTriangleNormal(triangle);
                            cubeSet[x, y, z] = true;
                            if (triangleNormal.z < 0 - ignoreNormalRange) {
                                cubeNormalSum[x, y, z]++;
                            } else if (triangleNormal.z > 0 + ignoreNormalRange){
                                cubeNormalSum[x, y, z]--;
                            }
                        }
                    }
                }
            }
        } else {
            for (x = startX; x < endX; ++x) {
                for (y = startY; y < endY; ++y) {
                    for (z = startZ; z < endZ; ++z) {
                        if (!IsAABCSet(x, y, z) && TriangleIntersectAABC(triangle, x, y, z)) {
                            cubeSet[x, y, z] = true;
                        }
                    }
                }
            }
        }
    }
    if(debug) {
        Debug.Log("Grid Evaluation Ended!");
        Debug.Log("Time spent: " + (Time.realtimeSinceStartup - startTime) + "s");
        Debug.Log("End: ");
    }
}

The code finds the AABB of each triangle (2), then performs the SAT intersection test on each cube intersected by AABB (3).

triangles (1) the triangle in the grid.  (2) the triangle with its AABB and the AABCs intersected by the AABB. (3) the AABCs intersected by the triangle

Filling the hollow inside

When this method is finished we will have a voxel model that reproduce the mesh. But we have not finished yet, we may need also to know which voxel (AABC) is inside the mesh and which is out. In order to do that we use the scan fill algorithm like the post on overgrowth blog explains, except for a little thing: we don’t start to fill the cube when the normal of the last triangle faces to the left, instead we mark ‘Begin’ and ‘End’ cubes in FillGridWithGameObjectMeshShell(). If the z component of the triangle is positive, we decrease cubeNormalSum[x, y, z] by one, else we increase it. When all the triangles have been processed, a  positive cubeNormalSum means that the cube is a ‘Begin’ cube, if it is negative then the cube is an ‘End’ cube.

We can’t just check the normal of the last triangle because we don’t know the order of the triangles, we neither traverse the entire grid during the creation of the voxel shell.

The method FillGridWithGameObjectMesh() does the real scan lining once that FillGridWithGameObjectMeshShell() ends. It traverses all the grid, starting from the cube at 0, 0, 0. If a ‘Begin’ cube is found, an ‘End’ cube is searched. If an ‘End’ cube is found, all the cubes between the last ‘Begin’ and ‘End’ are set.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

public function FillGridWithGameObjectMesh(gameObj : GameObject) {
   FillGridWithGameObjectMeshShell(gameObj, true);

   for (var x = 0; x < width; ++x) {
      for (var y = 0; y < height; ++y) {
         var fill = false;
         var cubeToFill = 0;
         for (var z = 0; z < depth; ++z) {
            if (cubeSet[x, y, z]) {
               var normalSum = cubeNormalSum[x, y, z];
               if (normalSum) {
                  if (normalSum > 0) {
                     // 'Begin' cube
                     fill = true;
                  } else {
                     // 'End' cube
                     fill = false;
                     while (cubeToFill > 1) {
                        cubeToFill--;
                        cubeSet[x, y, z - cubeToFill] = true;
                     }
                  }
               cubeToFill = 0;
             }
             continue;
         }
         if (fill) {
            cubeToFill++;
         }
      }
   }
}
 cubeNormalSum = null;
}

Performance

Performance are mainly determined by the number of triangles in the mesh and the side length of the AABCs. Here they are some of the tests made on my laptop:

Laptop specs: HP g6-1359el Intel Core i5-2450M - 2,5 GHz AMD Radeon HD 7450M

First Test

first

Mesh: construction_worke Time spent: 0.4051636s Triangles: 4020 Cube side: 0.05

Second Test

second

Mesh: construction_worker Time spent: 1.088864s Triangles: 4020 Cube side: 0.02

Third Test

third

Mesh: sphere

Time spent: 1.926165s Triangles:760 Cube side: 0.03

Memory could be saved storing cubeSet using a 3D bitarray class and cubeNormalSum using a 3D array of bytes

Try it yourself

For testing purpose there is also a VoxelizationTest.js script on my github. Attach it to an object with a mesh to try this voxelization script. Remember to enable Gizmos in the game window, otherwise the AABCs will not appear!

Comments